
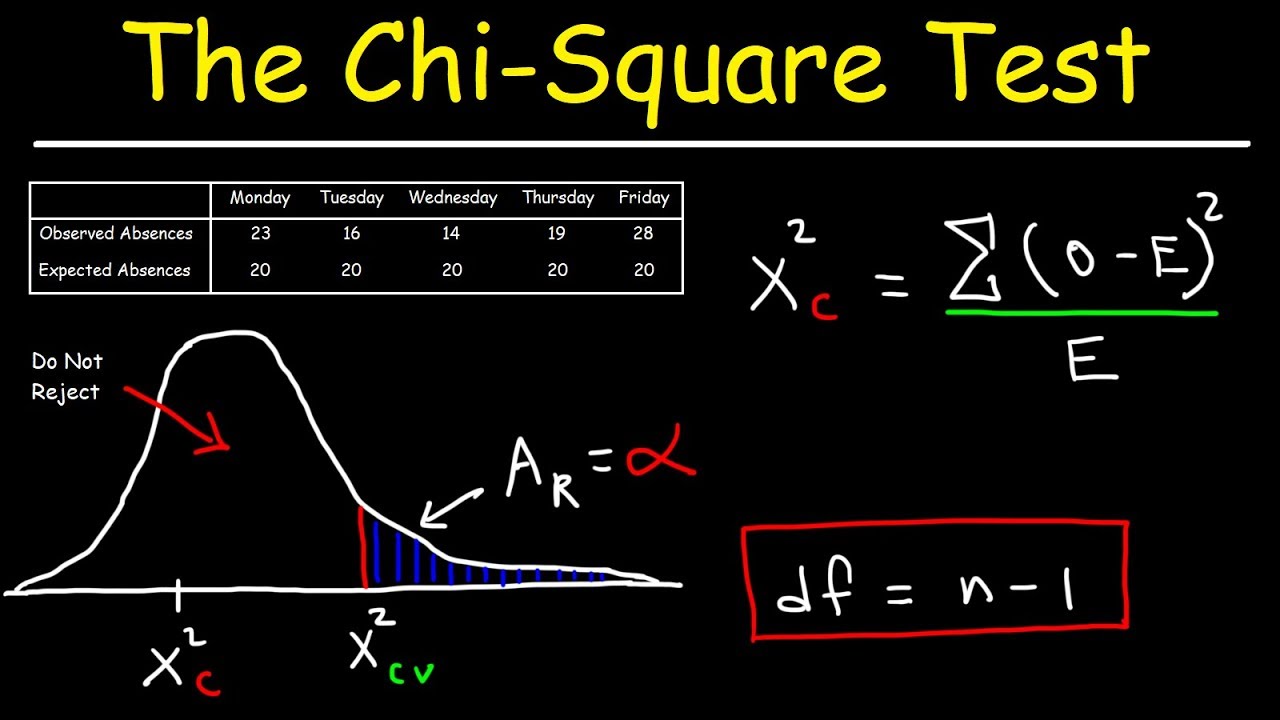
Recall that the Crosstabs procedure creates a contingency table or two-way table, which summarizes the distribution of two categorical variables. In SPSS, the Chi-Square Test of Independence is an option within the Crosstabs procedure. Before running the test, you must activate Weight Cases, and set the frequency variable as the weight.You should have three variables: one representing each category, and a third representing the number of occurrences of that particular combination of factors.The value in the "frequency" column for a given row is the number of unique subjects with that combination of categories.Each row in the dataset represents a distinct combination of the categories.Cases represent the combinations of categories for the variables.If you have frequencies (each row is a combination of factors):Īn example of using the chi-square test for this type of data can be found in the Weighting Cases tutorial. The categorical variables used in the test must have two or more categories. The dataset contains at least two nominal categorical variables (string or numeric).That is, each row represents an observation from a unique subject. Cases represent subjects, and each subject appears once in the dataset.Your data may be formatted in either of the following ways: If you have the raw data (each row is a subject): The categorical variables must include at least two groups. At minimum, your data should include two categorical variables (represented in columns) that will be used in the analysis.
#Chi square test degrees of freedom how to#
The format of the data will determine how to proceed with running the Chi-Square Test of Independence.
If you would like to learn how to do this test in R, read the article “ Chi-square test of independence in R”.Īs always, if you have a question or a suggestion related to the topic covered in this article, please add it as a comment so other readers can benefit from the discussion.There are two different ways in which your data may be set up initially.
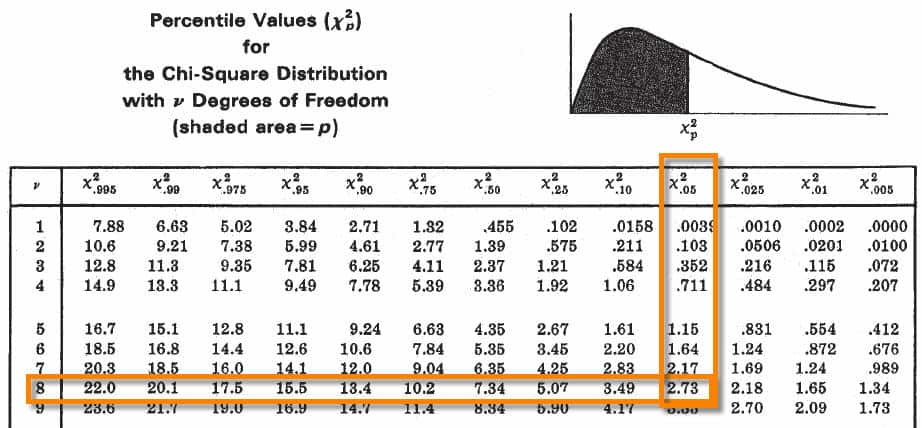
I hope the article helped you to perform the Chi-square test of independence by hand and interpret its results. Knowing the value of one variable helps to predict the value of the other variable. \(\Rightarrow\) This means that there is a significant relationship between the smoking habit and being an athlete or not. In our case, we can therefore reject the null hypothesis of independence between the two categorical variables at the 5% significance level. Like for many statistical tests, when the test statistic is larger than the critical value, we can reject the null hypothesis at the specified significance level. These expected frequencies are computed for each subgroup one by one with the following formula: We have the observed counts (see the table above), so we now need to compute the expected counts in the case the variables were independent. Remember that for the Chi-square test of independence we need to determine whether the observed counts are significantly different from the counts that we would expect if there was no association between the two variables. More on this critical value and the degrees of freedom later in the article. This critical value can be found in the statistical table of the Chi-square distribution.

This value, referred as the critical value, depends on the significance level \(\alpha\) (usually set equal to 5%) and on the degrees of freedom. The threshold between a small and large difference is a value that comes from the Chi-square distribution (hence the name of the test). On the other hand, if the difference between the observed frequencies and the expected frequencies is large, we can reject the null hypothesis of independence and thus we can conclude that the two variables are related. If the difference between the observed frequencies and the expected frequencies is small, we cannot reject the null hypothesis of independence and thus we cannot reject the fact that the two variables are not related. The Chi-square test of independence works by comparing the observed frequencies (so the frequencies observed in your sample) to the expected frequencies if there was no relationship between the two categorical variables (so the expected frequencies if the null hypothesis was true).


 0 kommentar(er)
0 kommentar(er)
